MTH252

Notes on Integration

Winter 2019

Chapter 4 from Calculus 1

§ 4-10 Antiderivatives

If the derivative is `2 x`, then what is `f(x)`?

I think it could be `f(x)=x^2+1`.

List antiderivatives for each of the following functions:

1. `5x^4`
2. `x^2-5x+1`
3. `sin(x)`
4. `sec^2(x)`
5. `e^{3x}`
6. `1/x`
7. `sqrt(x)`
8. `1/(1+x^2)`

§ 1-1 Approximating Areas

Consider the image below:

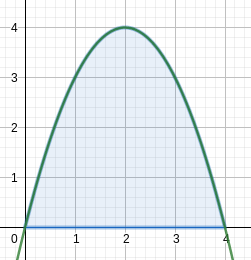
Positive area under a curve.

How do we find such an area?

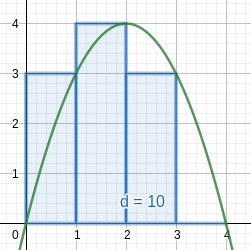
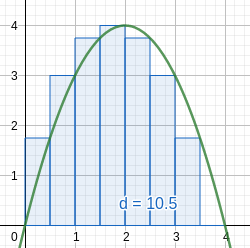
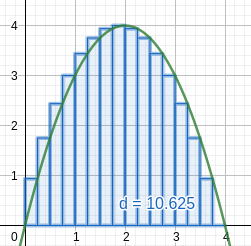
Rectangles are easy to work with.

Summation Notation

`sum_{i=1}^{20} i = 1+2+\cdots +19+20`

• Left Sums
• Right Sums
• Upper Sums
• Lower Sums
• Summation Rules
  • Constant
  • sum/difference
  • Multiple

Riemann Sums

`A~~sum_{i=1}^{n} f(x_i^\*) \Delta x`

Problems

Find the indicated area:

1. `f(x)=x^2` on `[0,4]`, 4 rectangles with left end-points
2. `f(x)=1/x` on `[0,4]`, 4 rectangles with right end-points
3. `f(x)=4x-x^2` on `[0,4]`, 4 rectangles with an upper sum
4. `f(x)=sin(x)` on `[0,pi]`, 6 rectangles with an upper sum and a lower sum.
5. `f(x)=x^2` on `[0,4]`, 8 and 16 rectangles with a right sum
6. `f(x)=x` on `[0,1]`, 100 rectangles with an upper sum